Final Performance Evaluation (Week 12)

This final post will begin by reviewing the most recent 4 week performance and then consider the whole 12 week investment period as a whole and evaluate the portfolio constructed on the client's behalf.

Below is the performance between week 8 and week 12 against the benchmark:

Returns for this period were quite negative, but as remarked in an earlier post negative absolute returns are not necessarily a sign of poor portfolio management - returns need to be considered relative to a benchmark. In this case the benchmark has performed considerably worse. The client's portfolio lost 1.71% whereas the benchmark index has fallen almost twice as much, by 3.34%. 

As noted in the previous post, adjustments made to the portfolio in week 8 did tend to reduce the duration of the holdings. Thus, perhaps the client's portfolio has mitigated losses in this period more effectively than the benchmark. Let's move on to consider the full sample of 12 weeks so that the data collected so far can be combined and analyzed in a more statistically significant manner.

Below is a the graph of performance over the full 12 weeks against the benchmark:

Surprisingly the constructed portfolio has outperformed the benchmark considerably. Looking at the full picture, this may due to the biggest price shifts occurring in the last 4 week period.

Overall, the client's portfolio returned 1.93% in 12 weeks. In comparison, the benchmark index returned only 0.33% due to poor performance in the last period.

Before assuming that this is enough to signify out-performance and claims of superior effective management, let's look first at how the performance is attributed in Bloomberg.

The attribution analysis shows that of the 1.60% excess returns compared to the benchmark, 0.78% was due to foreign exchange rate differentials, 0.66% was due to superior selection among individual assets, and 0.14% was due to improved allocation among sectors. 

The performance by attribution shows a more measured level of success in the management of the portfolio. One figure that is particularly pleasing is the 0.66% of active returns due to selection. This holds considerable significance because it was also the selection figure that showed superior returns in the 1 year backdating test (which showed +3.16% due to selection). I believe this shows a firm indication that the general diversification strategies employed have been effective. 

Let's continue on the the statistical summary over the 83 days of portfolio management:

These figures estimate the annualized mean return for the client's portfolio at 12.84%. This is certainly an impressive figure for a 100% fixed income portfolio tailored towards a low-medium risk profile.

Furthermore, the primary indicators for portfolio volatility show that the constructed portfolio was more consistent than the benchmark. The correlation measure has decreased compared to the backdated value of 0.89, this perhaps indicates some departure in strategy due to the implemented active management week 8 changes.

Overall, the evidence certainly suggests that the client's portfolio has been effectively diversified to achieve a returns comparable to those of a much larger index fund. In addition, a significant portion of the excess returns have been consistently attributed to the selection of stocks by the fund manager. Finally, the active management strategies implemented in week 8 showed promising results for further gains to be made if the client chooses to retain the portfolio management services provided over the past 12 weeks.

Provided below is the final composition of the portfolio in detail:

--

Performance and Adjustments (Week 8)

This post will take a quick look at the performance of the client's portfolio from week 4 to week 8 in order to see how effective the mean-variance optimization approach has proven. Also the structural effects of the changes made in week 8 will be summarized (see the previous post about forecasting interest rate changes for the rationale behind these new changes).

Graphed below is the portfolio performance against the benchmark over the past 4 weeks: 

Again, we are seeing highly comparable performance to that of the benchmark. A positive note to mark however is that instead of slight under-performance as in the first 4 weeks, there is now slight over-performance in this period. The return of the clients portfolio was 2.44%, compared to the 2.15% return of the benchmark index.

Overall, this seems like a good sign that the optimization of the portfolio has led to more fine-tuning of performance relative to the benchmark. It will be interesting to see once data up to 12 weeks is collected, how the performance is attributed by Bloomberg.

In the mean-time, here are the most recent changes made in week 8:

(Structural changes have been shaded in grey)

Overall, the average maturity of bonds in the portfolio has decreased. This is no surprise, as the active changes have been made in order to target changes in duration.

Looking at characteristics on a country level shows that modified duration of the Canadian segment has been dramatically decreased (now 5.05 from 9.86), the Euro segment has been decreased moderately (now 6.97 from 9.34) and the UK segment has been increased moderately (now 11.60 from 8.64).

--

Forecasting Interest Rate Changes

The goal of active portfolio management is to achieve excess returns. In order to achieve this we need to 'beat the market' by figuring out how certain bonds are under or over-priced given the current conditions.

No doubt the single greatest influence on corporate bonds is the effect of the term structure of interest rates. The term structure (i.e. the yield curve) indicates the rate at which the various cash flows associated with a bond should be discounted at, and thus determine its theoretical present value. Over terms at which the yield curve is higher, it suggests greater discounting and therefore lower contribution to present value. Thus forecasting changes to the yield curve will not only imply whether we should aim to increase or decrease modified duration within the portfolio, but also indicate exactly how this should be done, i.e. what structural changes should be made at each maturity.

Here is the current yield curve for Canadian Sovereign debt:

Suppose we forecast rates to increase across the entire term structure - what changes should we make the the selection of bonds by maturity?

Well, since bond prices will decrease as yields increase, we should aim to reduce exposure to rising interest rates by as much as possible. In terms of choosing between 5y, 10y, and 30y bonds - all higher maturity bonds should be discarded in favor of shorter 5y bonds. 


Below is the Eurozone yield curve:

Suppose this time we forecast a change in the way yields curve over maturities - what are the most appropriate adjustments to be made in response to this prediction?

Well, applying similar logic as above, we should invest more in 10y bonds (for which we expect prices to go up) and less in 30y bonds (for which we expect prices to go down). Note that there are also expected gains for 5y bonds, but not to the same extent as for 10y bonds according to this forecast.

Let's finally consider the UK yield curve for sovereign issues of debt:

Our forecast now is that yields will become lower in the future and that this will be more pronounced for over greater maturities.

This last forecast implies we should seek to increase allocations in 30y bonds (we expect prices to rise) and that we are most indifferent to shifting allocations away from 5y bonds.

Below is a summary for the changes suggested based on each of these forecasts. In total 6 bonds have been removed from the portfolio to be replaced by 6 newly selected bonds. If the forecasts made above turn out to be accurate then we can expect that these adjustments will improve the expected return on our portfolio over the last 4 weeks.




--

Performance and Adjustments (Week 4)

This post will take a first look into the actual realized performance of the constructed portfolio over the first 4 week period. Afterwards, the impact of the adjustments discussed in the previous post will also be looked into in more detail.

Below is the plotted returns of the client's portfolio compared to the benchmark:

The client's portfolio achieved a 1.31% return in this period compared to the 1.67% return of the benchmark. Looking at the plot of the performance difference, it can be seen that there was variation both above and below that of the benchmark. 

At this stage it would seem premature to read too much into the differences or to over analyse the small sample of data. Instead this first period of returns can act as a yardstick against which further adjustments made to the portfolio can be compared. What this first period does seem to imply is that under a simple 1/N passive investment strategy, the performance of the portfolio is similar to the benchmark.

Recall from the previous post that it has been decided to re-weight the allocation of funds within the portfolio on the basis of the mean-variance optimization results. Below are the adjusted weightings for the new allocation:

Lets also take a brief look at how this has changed the structure of the portfolio. Average maturity is now 9.5 years (up from 8.9 years in week 0), and similarly duration has also increased slightly. This means that over the next period we can expect the portfolio to react a bit more to changes in interest rates.

The characteristics by country are also provided below:

It seems that going forward the performance of the portfolio will be stronger tied to the performance of corporate bonds in Canada and Japan, as they now each contribute 35% weightings.

--

Markowitz Mean Variance Optimization

Markowitz (1952) was the first to demonstrate how portfolio managers could effectively minimize the risk of a portfolio for a given a desired return. For any attainable rate of return the portfolio may be weighted among the available assets for investment such that the overall volatility is minimized. 

Net volatility is not simply the sum of the volatilities of the individual assets, because as some rise in value others may tend to fall - such movements in opposing directions may partially cancel each other out and lead to 'smoother', less volatile returns. These many inter-relations are measured by the covariances between each asset and calculated based on historical return data. Thus for any achievable return, there is one or more optimal allocations of funds which minimizes volatility by choosing those assets least correlated with each other. Each such portfolio is termed an efficient portfolio and finding this optimal allocation for each level of achievable return maps out the efficient frontier of portfolios which lie on a parabola of risk-return as shown below.

To find the optimal weighting of assets within a portfolio requires extensive historical data on the return characteristics of the assets under consideration. Thus far, for the first four weeks of investment our portfolio has used equal weightings among each of the 40 corporate bonds among 6 different regions (Australia, Canadian, Europe, Japan, UK, US). Liu (2012) has collected data on the returns and correlations of corporate bonds from these same six regions. This county level data can be used to optimize the weightings within our portfolio and bring allocations closer to the efficient frontier. Our portfolio so far has held 17.5% weightings in Canadian, Europe, UK and US corporate bonds and 15% weightings in Australian and Japanese corporate bonds. 

The mean-variance optimization problem can be expressed mathematically as the following:

Since we require that our weightings are non negative (i.e. not allowing short sales) a computational approach will be applied to solve the above minimization problem. To ensure our portfolio remains internationally diverse let us further restrict the allocation of the portfolio to any one region to be between 5 and 35 per cent. Using the array functions in excel and then the solver function allows the efficient allocation to be determined for any given risk tolerance. The graphic below shows the results of such analysis, showing how the efficient allocation between regions changes as the risk tolerance increases from 0 to 15.

At the lowest risk tolerance levels of 0 or 1 it can be seen that the efficient allocation of the portfolio is given by 35% Australian bonds, 35% Japanese bonds, 15% European bonds, and 5% for each Canadian, US, and UK bonds. As risk tolerance increases to 5 the portfolio shifts away from Australian bonds and towards Canadian bonds. At an even higher risk tolerance levels of 9 the major holdings are in Canadian and European bonds. As risk tolerance continues to increase to the highest levels holdings of US bonds continue to increase until the portfolio is primarily comprised of Canadian and US holdings. The historical data suggests that holdings of UK bonds should remain at the minimum level of 5% as greater returns for a given level of risk can be found in corporate bonds of other regions.

Through our risk tolerance surveys of the client it was determined that they have a below average risk tolerance. For this reason, a risk tolerance of 5 has been chosen as a suitable estimate to rebalance the portfolio more efficiently among regions. This requires an adjustment to our portfolio by increasing Canadian and Japanese bond holdings to 35%, decreasing European bonds slightly to 15% and decreasing all other holdings (Australia, UK, US) down to 5%.

--

Portfolio Characteristics (Week 0)

This post will look in more detail at the characteristics of the portfolio of corporate bonds constructed and also see how the portfolio performs in a one-year backdate test.

The table below shows the full details of each of the bonds hand picked for the portfolio. Individual bonds were not selected based on their coupon rates or yield-to-maturity. Instead, bonds were selected according to the diversification criteria discussed in the previous blog post.

Looking at the summary of holdings below gives a quick indication that bonds are fairly evenly spread across denominations in 6 different currencies. Furthermore, each individual bond has been assigned the same weighting; each of the 40 stocks chosen were allocated weightings of 2.5%. This follows the simple 1/N allocation strategy.

The view below in Bloomberg has been customized to analyse the portfolio by currency segments. It can be seen that the Australian segment of bonds has significantly lower average maturity (Mty=5.23 yrs) and thus also lower modified duration (ModDur=4.45). Modified duration gives a first order approximation for how the bond's price will react to a 100 basis point change in interest rates. If interest rates in Australia were to rise by 1%, this figure predicts a 4.45% drop in the price of the bonds. 

The Australian bonds had lower maturities since there were no AUD denominated bonds at longer maturities. Most Australian bonds at longer maturities were denominated in USD. So this is largely an artifact of the selection rules applied to the portfolio. It will be interesting to note whether the AUD segment performs comparatively better if a general decline in interest rates is observed.

A replicate of the portfolio has also been constructed one year prior so that the backdated performance of the portfolio can be analysed between 17/02/14 and 17/02/15. Backdating is certainly not the most reliable measure of future performance, but it is a useful procedure for getting a feel for what expectations we should have about the portfolio. 

Furthermore, backdating is useful to determine a suitable choice of benchmark. Without a benchmark for comparison it is not possible to evaluate the performance of a portfolio. For instance, say the value of the portfolio falls by 2% over the next month. A stand-alone absolute figure like this does not inform us on whether that is a good or bad result. If other comparable portfolios had lost 5% over the same period, even this loss could indicate a well managed fund.

Below is the backdated performance of the portfolio against the Bloomberg Global Investment Grade Corporate Bond Index (BCOR). This portfolio was chosen since it holds the most diversified holdings among the indices considered, with considerable holdings across each of the countries included in the client's portfolio.

Looking at these return graphs performance shows that there is a high degree of correlation between the two funds (in fact that correlation is 0.89, as shown in the statistical summary below). This is a good sign as it seems the benchmark chosen is an appropriate one. While both funds showed solid performance, over the past year the returns of the constructed portfolio fell short of the benchmark by approximately 1%.

The attribution tab in Bloomberg can help break down the performance further:

According to the attribution results there was a large difference in returns attributable to currency exposure. It seems despite issues from a wide selection of countries, the benchmark contains mostly (~60%) bonds denominated in USD. Since the USD performed comparatively well over this period the benchmark achieved 5.15% greater returns from exchange rate exposure (performance is being measured in pounds sterling).

As for the allocation of stocks among sectors and the selection of individual stocks, Bloomberg's analysis is very favorable of the constructed portfolio. In fact, it outperformed the benchmark by a significant 3.16% in terms of selecting individual stocks.

Looking at the statistical summary above, it also seems that the constructed portfolio experienced lower volatility in its returns. Running a simulation analysis, supports this evidence further. The 5% Value at Risk (daily) for the portfolio is simulated at £5,150 compared to £5,706 for the benchmark index.

--

Constructing a Fixed Income Portfolio

When first constructing a portfolio, there is a whole host of questions that the fund manager must consider. The answer they give to these questions will determine the efficiency of their investment strategy. 

What proportion of cash, bonds, and equities should be held?

What is the appropriate risk vs reward balance that we should aim for?

How many assets are required to reap diversification benefits?

Should we invest in domestic or foreign assets? Should they be hedged?

What is the time horizon of our investment? How much liquidity is required?

How should the weightings of the assets held be determined?

Which sectors should we invest in? Corporate or government?

How often should adjustments be made to the portfolio holdings?

This post will seek to answer the above questions and in the process develop a strategy for the construction of a fixed income portfolio for a hypothetical client. Since our client is at retirement age, they have requested a portfolio entirely composed of fixed income assets. Investing in government bonds would certainly be a minimal risk strategy, however to better match the risk profile of the client it has been decided to invest instead in corporate bonds. Relative to equities bonds yield returns with much lower volatility so such a portfolio will naturally be low risk. The risk tolerance of the investor was measured as slightly-below average, but not extremely low. For this reason, 90 per cent of the portfolio will be comprised of investment grade bonds (rated BBB+ or greater) and 10 per cent of the portfolio will be comprised of high yield bonds (BBB or lower). 

The next decision to make is how many assets to hold within the portfolio. Dbouk & Kryzanowski (2010) examine the diversification benefits associated with different-sized portfolios of bonds using various metrics. They examine the marginal diversification gains by industry sector, credit ratings, and maturity. In general, they find that the optimal portfolio size is about 40 bonds with associated diversification benefits of about 80%. For this reason the portfolio will be constructed by selecting 40 different corporate bonds.

Research by Liu (2012) investigates whether US investors can achieve diversification benefits by adding international corporate bonds to their portfolio. His findings show that such an approach can significantly reduce portfolio volatility and increase Sharpe ratio, reducing risk by as much as 82.4 per cent. Based on these findings the portfolio to be constructed will be diversified among British, American, Australian, Canadian, European, and Japanese corporate bonds. The bonds purchased will be issued in foreign currency, and as such appropriate currency hedges will be employed (to be discussed further in a later post).

Next, we must consider the appropriate time horizon of our investment portfolio and the liquidity requirements of the client. The client has indicated that they may require access to some portion of the funds after 5 years. For this reason, at least half of the bonds selected for the portfolio will have maturities of approximately 5 years. 

The weighting strategy of the portfolio will follow a simple 1/N strategy, whereby equal allocation values are maintained for each asset. While this simple portfolio strategy does not optimize with respect to any return information, it is easy to implement and not subject to any bias.  DeMiguel, Garlappi, and Uppal (2009) show that across a large class of sample based mean variance portfolio allocation models, no model consistently out performs the 1/N naive portfolio allocation strategy in out of sample performance. 

Finally, it is worth considering the industry sectors chosen for investment. The focus of the diversification strategy employed so far is primarily geographical with some consideration given to choosing bonds of different maturities. As such, sector diversification has been deemed of lesser importance. However, where possible bonds from a range of different sectors have been selected for each country. 

The portfolio was constructed using the PRTU function in Bloomberg.

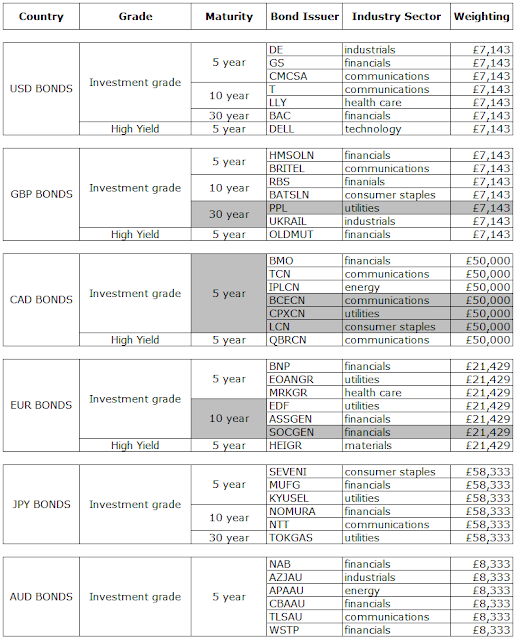
Here is a breakdown of the bonds chosen by country, maturity, and industry:

--

Risk Tolerance and Capacity for Loss

The Financial Services Authority (FSA) is responsible for the regulation of financial services in the UK. In 2011, the FSA released a guidance paper on suitable investment selection procedures for independent financial advisers. The paper called for advisers to distinguish clearly between the risk preferences and risk capacity. 

The FSA defines capacity for loss as "the customer’s ability to absorb falls in the value of their investment", and suggests that "if any loss of capital would have a materially detrimental effect on their standard of living, this should be taken into account in assessing the risk that they are able to take". In contrast risk tolerance (or alternatively attitude to risk) can be defined as "the maximum amount of uncertainty that someone is willing to accept when making a financial decision" (Grable, 2000). Clearly, the distinction between the two measures is that capacity for loss measures how much risk the investor is able to take whereas attitude to risk aims to measure how much risk the investor is willing to take. 

The two aspects of risk are best illustrated through an example. Below is a description of a hypothetical investor who wishes to invest £1,000,000 in a fixed income portfolio:

The client is a male 55 year old semi-retired doctor. He co-owns his own practice, with his share valued at £320,000. He currently works a 4 day week, earning £90,000 per annum, but expects to be cutting down his hours further in the years to come. He has a wife and three adult children, with only one of the children still living at home. Their house is valued at £300,000 and the combined value of their two cars is £80,000. His wife is a retired academic, but she occasionally volunteers at local universities as a guest lecturer. The investor would like to know that his funds are reasonably secure and will provide primarily income with some element of capital appreciation. At present the client does not envisage requiring access to their funds for at least 5 years but they may reserve the right to re-visit this. When he retires fully, in perhaps 5 to 10 years time, the client plans on selling his share of the medical practice and buying a medium sized luxury yacht.

From the above description the factors which likely affect the client's attitude to risk and capacity for loss can be distinguished:

Factors affecting attitude to risk Male Retirement age Married Highly educated High income, currently £90,000 / yr Respected occupation

Factors affecting capacity for loss Income stream for the next 5-10 yrs Value of investment: £1,000,000 Value of assets: £700,000 Expected future expenses (yacht) High living standard to maintain High social status to maintain

Research suggests that males are more risk tolerant than females, as are those with higher attained education, higher income, greater financial knowledge and more professional occupations (Grable, 2000). Age also plays a significant role, and it is generally accepted that risk tolerance decreases with age. Hallahan, Faff, & McKenzie (2004) found that psychometric Risk Tolerance Scores (RTS) decrease non-linearly with age, as shown in the figure below: 

This highlights how an investor's risk preferences may change with time and may need to be reassessed as they progress towards later stages of life. The hypothetical client described above is 55 years old, and therefore would look for greater security in his investment portfolio despite the other factors which may otherwise indicate a very high risk profile.

To best tailor the portfolio to the client's requirements a valid and reliable estimate of their risk tolerance level is required. One such tool is the Grable and Lytton (1999) Risk Tolerance Scale. Provided below is the risk tolerance quiz used by Grable and Lytton, which you can use to estimate your own risk tolerance profile. How does it compare with the score of the 55 year old doctor below? What might be the reasons for these differences?

Risk Tolerance estimate for the client: (22) = Below-average risk tolerance

Investment Risk Tolerance Quiz (Grable and Lytton, 1999)

1. In general, how would your best friend describe you as a risk taker?

(1)  A real risk avoider

(2)  Cautious 

(3)  Willing to take risks after completing adequate research

(4)  A real gambler

2. You are on a TV game show and can choose one of the following. Which would you take?

(1)  $1,000 in cash

(2)  A 50% chance at winning $5,000

(3)  A 25% chance at winning $10,000

(4)  A 5% chance at winning $100,000

3. You have just finished saving for a "once-in-a-lifetime" vacation. Three weeks before you plan to leave, you lose your job. You would:

(1)  Cancel the vacation

(2)  Take a much more modest vacation

(3)  Go as scheduled, reasoning that you need the time to prepare for a job search

(4)  Extend your vacation, because this might be your last chance to go first-class

4. If you unexpectedly received $20,000 to invest, what would you do?

(1)  Deposit it in a bank account, money market account, or an insured CD

(2)  Invest it in safe high quality bonds or bond mutual funds

(3)  Invest it in stocks or stock mutual funds

5. In terms of experience, how comfortable are you investing in stocks or stock mutual funds?

(1)  Not at all comfortable 

(2)  Somewhat comfortable 

(3)  Very comfortable

6. When you think of the word "risk" which of the following words comes to mind first?

(1)  Loss 

(2)  Uncertainty 

(3)  Opportunity 

(4)  Thrill

7. Some experts are predicting prices of assets such as gold, jewels, collectibles, and real estate (hard assets) to increase in value; bond prices may fall, however, experts tend to agree that government bonds are relatively safe. Most of your investment assets are now in high-interest government bonds. What would you do?

(1)  Hold the bonds 

(2)  Sell the bonds, put half the proceeds into money market accounts, and the other half into hard assets 

(3)  Sell the bonds and put the total proceeds into hard assets 

(4)  Sell the bonds, put all the money into hard assets, and borrow additional money to buy more

8. Given the best- and worst-case returns of the four investment choices below, which would you prefer?

(1)  $200 gain best case; $0 gain/loss worst case 

(2)  $800 gain best case; $200 loss worst case 

(3)  $2,600 gain best case; $800 loss worst case 

(4)  $4,800 gain best case; $2,400 loss worst case

9. In addition to whatever you own, you have been given $1,000. You are now asked to choose between:

(1)  A sure gain of $500 

(2)  A 50% chance to gain $1,000 and a 50% chance to gain nothing

10. In addition to whatever you own, you have been given $2,000. You are now asked to choose between:

(1)  A sure loss of $500 

(2)  A 50% chance to lose $1,000 and a 50% chance to lose nothing

11. Suppose a relative left you an inheritance of $100,000, stipulating in the will that you invest ALL the money in ONE of the following choices. Which one would you select?

(1)  A savings account or money market mutual fund 

(2)  A mutual fund that owns stocks and bonds 

(3)  A portfolio of 15 common stocks 

(4)  Commodities like gold, silver, and oil

12. If you had to invest $20,000, which of the following investment choices would you find most appealing?

(1)  60% in low-risk investments 30% in medium-risk investments 10% in high-risk investments 

(2)  30% in low-risk investments 40% in medium-risk investments 30% in high-risk investments 

(3)  10% in low-risk investments 40% in medium-risk investments 50% in high-risk investments

13. Your trusted friend and neighbor, an experienced geologist, is putting together a group of investors to fund an exploratory gold mining venture. The venture could pay back 50 to 100 times the investment if successful. If the mine is a bust, the entire investment is worthless. Your friend estimates the chance of success is only 20%. If you had the money, how much would you invest?

(1)  Nothing 

(2)  One month's salary 

(3)  Three month's salary 

(4)  Six month's salary

Add up all of the blue numbers for each of your responses. In general, the score that you receive can be interpreted as follows:

(18) or below = Low risk tolerance

(19) to (22) = Below-average risk tolerance

(23) to (28) = Average/moderate risk tolerance

(29) to (32) = Above-average risk tolerance
(33) and above = High risk tolerance

--